To most students, multiplying fractions is the easiest of the four basic operations. Why? You do not have to worry about a common denominator.
Here’s the Rule for Multiplying Fractions...
-
- Multiply numerators.
- Multiply denominators.
- Simplify or reduce the results, if needed.
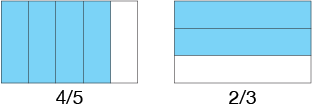
We can illustrate the multiplication problem below by picturing each fraction as part of a whole or unit. With that idea in mind, we can show the fractions 4/5 and 2/3 as…
4/5 X 2/3 = (4 X 2)/(5 X 3) = 8/15
Like in our example above, we wanted to find 2/3 of 4/5. The “of” in this expression indicates that we are taking a part of something. That’s what multiplying fractions is really all about.
When we combine the two diagrams as shown below, the part of the whole that represents multiplying 2/3 x 4/5 is shown in the double-shaded area.
2/3 x 4/5 = 8/15
Notice how the rule is “suggested” by the diagram.
By the way…
-
- Did you also notice that the double shaded area is less than both fractions, 2/3 and 4/5? That’s because multiplying proper fractions always produces a smaller fraction.
- When we multiply a fraction by a fraction, aren’t we actually taking a “part” of a “part“?
- As always, don’t forget to reduce or simplify your answer, as needed.
- Present your solution in the form asked for in your instructions.
Homework Helpers
Check out these great additional resources for multiplying fractions: Reducing Fractions and Simplifying Fractions
Related Topics
If you’ve mastered multiplying fractions, why not try your hand at one of the following: Dividing Fractions, Adding Fractions or Subtracting Fractions
Fraction Calculator
Learn how to solve fraction problems, then check your work with our online fraction calculator. Click here >
Fraction Worksheets
Free downloadable worksheets make it to easy to practice multiplying fractions. To get even more fraction worksheets, click here >
[wpdm_file id=9]